I. Co to jest sztuczna inteligencja i do czego się może przydać medykom.
II. Przykłady zastosowań sztucznej inteligencji w medycynie - 4 godz.
Pojęcia nie dają się precyzyjnie opisać - ogólny problem związany z kateogryzacją.
Pacjent nie jest "chory/zdrowy" lecz może być chory w różnym stopniu, symptomy występują w różnym stopniu, ciśnienie może być bardzo niskie, niskie, średnie, normalne, dobre, wysokie, bardzo wysokie itp. Jak ma rozumieć takie pojęcia system ekspercki?
Logika klasyczna nie jest dobrym językiem do opisu zagadnień medycznych, logika wielowartościowa lub jej uogólnienia są lepsze.
Wnioskowanie statystyczne i metody probabilistyczne - alternatywne rozwiązanie do logiki.
Metody Bayes’owskie: prawdopodobieństwo P(Hi|E) prawdziwości hipotezy Hi przy danej ewidencji E wyraża się wzorem:
Sieci Bayes'owske: wnioskowanie probabilistyczne logiczne + sieci semantyczne. Pokazują związki probabilistyczne pomiędzy symptomami a chorobą, chociaż nie zawsze są to związki przyczynowe, często jedynie korelacje.
Opisując przypadek za pomocą słów musimy odwłać się do jakiejś formy logicznego wnioskowania. Informacja, którą mamy do dyzpozycji często jest niepewna, prawdopodobna, częściowa.
Logika niemonotoniczna: dodanie nowej wiedzy może zmienić prawdziwość wcześniej ustalonych faktów. Proceduralna reprezentacja wiedzy często prowadzi do takich problemów.
Logika wielowartościowa, Łukasiewicz i Tarski, wielostopniowe tak/nie. Dobry pomysł ale rzadko stosowany.
Częściowa przynależność do zbioru - np. jest "w pewnym stopniu" łysy albo chory. Stopień przynależności określić można np. procentowo, dla typowego przypadku może on wynosić 100% a dla przypadków na granicy być poniżej 50%.
Definicja formalna zbioru rozmytego:
Dla danego podzbioru A zbioru X i funkcji c: X ® [0,1] zbiór par (x, cA(x)) nazywa się zbiorem rozmytym X.
Funkcja cA(x), przynależności x do A; określa stopień, w jakim x należy do A. Zbiór rozmyty jest więc zbiorem elementów i stopni przynależności tych elementów do danego zbioru.
Np. dla ciśnienia krwi można zdefiniować zbiór DSN="duże w stopniu niepokojącym" podając średnią wartość ciśnienia uznanego za DSN określoną przez paru ekspertów i przypisując wartości przynależności 0 jako minimalne, określone przez ekspertów. Pośrednie wartości funkcji przynalezności moga zmieniać się liniowo.
Typowe funkcje przynależności w logice rozmytej to funkcje trójkątne lub trapezoidalne.
Relacje porządku, sumowanie, iloczyn, dopełnienie etc. dla zbiorów rozmytych można zdefiniować na wiele sposobów; np. najczęściej suma A+B dwóch zbiorów rozmytych odpowiada alternatywie logicznej, za funkcje przynależności brać można maksium wartości cA(x)+ cB(x), lub dowolną rosnącą monotoniczną funkcję obu tych wartości, a dla iloczynu brać mozna minimum lub iloczyn obu wartości. Dlatego istnieje wiele możliwych realizacji logiki rozmytej.
Logika rozmyta jest bardzo popularna w systemach medycznych i zastosowaniach technicznych.
Zbiór elementów, które na pewno należą i tych, które na pewno nie należą - trapezoidalen funkcje przynależności.
Zbiory przybliżone: zdefiniowane przez zbiór elementów, które napewno należą i na pewno nie należą do danego zbioru.
Zbiór obiektów ob, zbiór atrybutów AT, zbiór wartości atrybutów V, funkcja (predykat)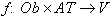 
przypisująca obiektom i ich atrybutom jakieś wartości.
Relacja równowartości R(A), gdzie A Í AT, obiekty o1 i o2
Wówczas obiekty o1 i o2 są nierozróżnialne z punktu widzenia atrybutów z A. Np. dwie chore osoby moga mieć bardzo podobne symptomy i wóczas przypiszemy je do jednej klasy.
Klasy równoważności: {e0, e1, e2, ... , en} = R(A)*, czyli wszystkie obiekty o takich samych wartościach predykatów na nich zdefiniowanych tworzą nową klasę.
Para (O, R) tworzy przestrzeń aproksymacji (koncepcji).
O Í Ob można aproksymować przez sumę klas tworząc przybliżenie dolne (obszar pozytywny):
Przybliżenie górne, nazwane rejonem negatywnym
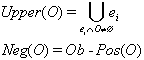
Różnica tych przybliżeń stanowi granicę (boundary)
Zbiór przybliżony to taki, którego granica jest niepusta.
Jeśli zbiór atrybutów A wystarczy by utworzyć partycję R(A)* która dokładnie definiuje O to nazywamy go reduct.
Iloczyn wszystkich zbiorów reduct nazywamy jądrem (core).
POS(O) ® klasa przypadków pozytywnych
NEG(O) ® klasa przypadków negatywnych
BND(O) ~~® (prawdopodobnie) klasa przypadków pozytywnych
Najprostszy przykład zastosowania logiki przybliżonej:
| Pacjent | Ból głowy | Ból mięśni | Temperatura | Grypa |
1. Jaś | nie |
tak | wysoka |
tak |
2. Małgosia | tak | nie | wysoka | tak |
| 3. Piotr | tak | tak | b. wysoka | tak |
| 4. Paweł | nie | tak | normalna | nie |
| 5. Karol | tak | nie | wysoka | nie |
| 6. Kaśka | nie | tak | b. wysoka | tak |
Ból głowy - nierozróżnialni pacjenci 1,4,6 oraz 2,3,5;
Małgosia i Karol - takie same symptomy, przypadki graniczne.
Pozytywne przykłady osób z grypą: O = {Jaś, Małgosia, Piotr, Kasia}
Negatywne przykłady osób z grypą: O = {Paweł, Karol}
Zbiór atrybutów: A = AT = {BG, BM, T}
Klasy: R(A)* = {{Karol, Małgosia}, {Jaś}, {Piotr}, {Paweł}, {Kasia}}
Ograniczenie dolne: Pos(O) = Lower(O) = {Jaś, Piotr, Kasia}
Obszar negatywny: Neg(O) = {Paweł}
Granica: Bnd(O) = {Karol, Małgosia}
Apr. górna: Upper(O) = Pos(O) + Bnd(O) = {Jaś, Małgosia, Piotr, Paweł, Kasia}
Dokładność (ostrość) koncepcji “ma grypę”: |Lower(O)| / |Upper(O)| =3/5,
Dokładność koncepcji “nie ma grypy”, |Neg(O)| / |Lower(O)| = 1/3.
Wartości funkcji przynależności do zbioru “ma grypę”: 1, 1/2, 1, 0, 1/2, 1.
Reguły decyzji (przynależności do klasy “ma grypę”):
IF (ból głowy =F i temperatura = wysoka) THEN grypa =T
IF (ból głowy =T i temperatura = wysoka) THEN grypa =T
IF (ból głowy =T i temperatura = b. wysoka) THEN grypa =T
IF (ból głowy =F i temperatura = normalna) THEN grypa =F
IF (ból głowy =T i temperatura = wysoka) THEN grypa =F
IF (ból głowy =F i temperatura = b. wysoka) THEN grypa =T
Granice decyzji klasyfikatorów opartych na logice klasycznej, rozmytej i przybliżonej wyglądają w dwóch wymiarach następująco:
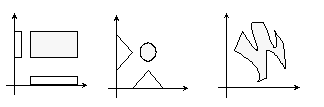
Dla logiki klasycznej mamy prostokątne granice, dla rozmytej z trójkątnymi funkcjami są one okrągłe, ale opis danej choroby przez dwa parametry (np. wyniki testów) może wymagać znacznie bardziej skomplikowanych granic decyzji (ostatni obrazek). Potrzeba wówczas wiele reguł lub konieczne są bardziej złożone systemy kasyfikacyjne.
W ostatnich latach również "intuicja" eksperta została w pewien sposób uchwycona w systemach, które uczą sie na przykładach. Jeśli zgromadzimy dostatecznie dużo dobrze zdiagnowonych opisów można na ich podstawie stworzyć system, który wykorzysta podobieństwo do istniejących przypadków lub nauczy się istotnych zależności, potrzebnych do diagnozy.
Najbardziej popularne metody uczące się to: metody oparte na podobieństwie, drzewa decyzji i sieci neuronowe.
Uogólnienia: uśrednij wynik dla kilku najbardziej podobnych przypadków; wprowadź lepsze funkcje podobieństwa, sprawdź, które testy są najbardziej istotne.
Jeśli chcemy oddzielić przypadki jakieś klasy od pozostałych musimy znaleźć taką cechę, która pozwala je maksymalnie różnicować. Jeśli uda nam się znaleźć wartość graniczną jakiejś cechy, powyżej której będziemy mieli maksymalnie dużo wektorów z danej klasy, a poniżej wektorów z klas przeciwnych, to dokonamy wstępnego podziału wszystkich przypadków na dwa podzbiory, które powinny być prostsze do analizy. Dla każdego z tych podzbiorów będziemy dalej poszukiwać najlepiej różnicującego testu. Powstanie w ten sposób drzewo decyzji, którego korzeń (węzeł początkowy) reprezentować będzie sytuację wyjściową (pełny zbiór).
Z korzenia wychodzą co najmniej dwie krawędzie do węzłów leżących na niższym poziomie, reprezentujących podzbiory danych podzielone za pomocą jakiegoś testu. Z każdym węzłem związane jest pytanie o wartość cechy, czyli Test mający wartość logiczną Tak-Nie, lub mający kilka wartości. Węzły końcowe, z których nie wychodzą już żadne krawędzie, nazywane są liśćmi. Powinny one zawierać wektory tylko z jednej klasy.
Wszystkie metody tworzenia drzewa decyzyjnego mają bardzo podobną konstrukcję, której szkielet można przedstawić za pomocą następującego algorytmu:
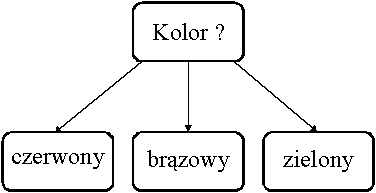
Ostatecznie wybierany jest próg, który prowadzi do najlepszej wartości kryterium podziału.
Bardzo istotnym elementem w tworzeniu drzewa decyzyjnego jest wybranie cechy lub też liniowej kombinacji cech, w oparciu o które nastąpi podział zbioru obiektów. W celu określenia jakości podziału stosuje się miary zróżnicowania podzbioru w wyniku podziału. W takim przypadku poszukujemy podziału, który minimalizuje miarę zróżnicowania. Najczęściej wykorzystywaną funkcją zróżnicowania jest funkcja mierząca ilość zdobytej w wyniku podziału informacji (funkcja entropii):
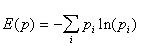
gdzie liczby pi określa się na podstawie częstości występowania wektorów należących do różnych klas w podzdbiorach powstałych w wyniku podziału. Wiele eksperymentów porównawczych wykazuje, że jest to najbardziej uniwersalna miara. Oprócz miar opartych na entropii stosuje się również statystyczne miary podobieństwa.
W praktycznych zastosowaniach dane często zawierają szum - wartości błędnie zapisane lub niektóre przypadki błędnie sklasyfikowane. Szum prowadzi do tworzenia bardzo złożonych drzew, które próbują szczegółowo opisać anomalie w danych. Większość systemów radzi sobie z tym problemem poprzez upraszczanie początkowego drzewa, polegające na wyszukiwaniu podgałęzi mających niewielki wpływ na dokładność klasyfikacji i zastąpienie tych podgałęzi liściem. Istnieje wiele metod stosowanych w drzewach decyzyjnych do znalezienia kompromisu pomiędzy dokładnością klasyfikacji na zbiorze treningowym a złożonością drzewa, jak np. stosowana w algorytmie C4.5 metoda MDL (Minimum Description Length), czy też metoda MCP (Minimal Cost-complexity Pruning) stosowana w drzewach CART. Metody te zakładają, że model opisujący nasze dane powinien być jak najprostszy, należy więc zmniejszać całkowitą długość wszystkich gałęzi drzewa decyzji (MDL) lub usuwać te fragmenty gałęzi (MCP), które powodują nieznaczne zwiększenie się liczby błędów. W efekcie na danych treningowych liczba błędów może wzrosnąć, system przestanie bowiem poprawnie klasyfikować szum w danych, ale na danych testowych rezultaty powinny się poprawić.
Z geometrycznego punktu widzenia drzewa klasyfikacyjne są podobne do używanych w statystyce liniowych funkcji dyskryminacyjnych, gdyż dzielą wielowymiarową przestrzeń cech hiperpłaszczyznami po to, by wyodrębnić obszary, w których występują tylko elementy z jednej klasy. Na podstawie drzewa decyzyjnego bardzo łatwo jest określić reguły przynależności obiektu do danej klasy. Reguły takie tworzy się na podstawie ścieżki prowadzącej od korzenia do liścia. Zwykle jedna z klas – najbardziej niejednorodna - wybierana jest jako klasa domyślna (default). Obejmuje ona wszystkie przypadki, które trudno jest opisać za pomocą prostego zestawu warunków.
Sztuczna sieć neuronowa jest zbiorem połączonych ze sobą węzłów przetwarzających dochodzącą do nich informację i przesyłających wyniki swoich obliczeń do dalszych węzłów. Węzły te nazywa się umownie neuronami, gdyż sposób ich pobudzenia wzorowany jest zwykle na biologicznych neuronach: dochodzące do neuronu sygnały są sumowane z uwzględnieniem parametrów odpowiadających wagom synaptycznym. Taka ważona suma określa całkowite pobudzenie, czyli aktywację neuronu. Inny sposób określania aktywacji neuronów polega na porównywaniu struktury dochodzącego sygnału z sygnałem wzorcowym – neuron reaguje tylko na sygnały podobne do tych, których się wcześniej nauczył. Funkcję, przekształcającą dochodzące do neuronu dane na odpowiedzi neuronu, nazywa się funkcją transferu. Funkcja transferu zależy zwykle w nieliniowy sposób od aktywacji neuronu, może się np. zmieniać skokowo gdy aktywacja przekroczy pewien próg.
W sieci wyróżnia się jednostki wejściowe, do których wprowadzane są dane, oraz jednostki wyjściowe, których aktywność interpretuje się jako rezultat działania sieci. Pozostałym neuronom, zwanym neuronami ukrytymi, i połączeniom pomiędzy wszystkimi neuronami, przypisuje się parametry, których wartości decydują o sposobie działania sieci. Parametry te mogą ulegać zmianie w celu zwiększenia poprawności działania sieci – proces ten nazywa się uczeniem sieci. Typowa struktura sieci dla 3-wymiarowych wektorów danych, dwóch warstw ukrytych neuronów i jednej jednostki wyjściowej, pokazana jest na rysunku.
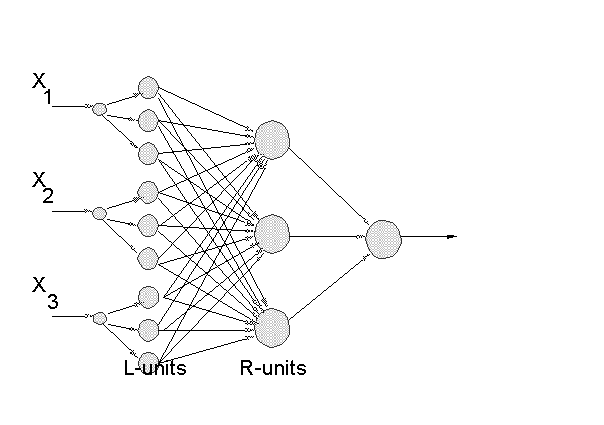
Algorytm uczenia “pod nadzorem” (supervised, czasem używa się też określenia “z nauczycielem”) oznacza, że w ciągu treningowym obok wektorów, które podawane są na wejście sieci, występują rozwiązania, czyli to co powinno pojawić się na wyjściu (algorytmy bez nadzoru same usiłują wykryć, na jakie klasy najlepiej podzielić wprowadzane dane). Algorytmy konstruktywistyczne charakteryzują się tym, że określenie topologii sieci (sposobu połączeń jej elementów) jest częścią tych algorytmów. Stosuje się dwie techniki konstruowania takich sieci. Pierwsza z nich polega na tworzeniu sieci od zera, tzn. na początku istnieje tylko warstwa wejściowa i wyjściowa, natomiast warstwy ukrytej nie ma wcale lub też jest, ale z niewielką liczbą węzłów. Następnie w trakcie uczenia stopniowo dostawiane są kolejne neurony oraz ewentualnie kolejne warstwy ukryte. Druga metoda polega na rozpoczęciu z siecią posiadającą dużą (nadmiarową) liczbą węzłów, które w miarę możliwości zostają później usuwane. Dużą zaletą podejścia konstruktywistycznego jest to, że nie trzeba samemu ręcznie dobierać liczby neuronów oraz liczby warstw ukrytych, co niekiedy wymaga wielu prób i może być bardzo czasochłonne. Kluczowym elementem w algorytmach konstruktywistycznych jest określenie momentu w trakcie uczenia, w którym trzeba dostawiać (usunąć) węzeł ukryty.
Sieć oparta na konstruktywistycznym algorytmie zawsze może nauczyć się klasyfikacji danych treningowych w 100% poprawnie. Celem uczenia jest jednak znalezienie sieci, która na podstawie znajomości zbioru wektorów treningowych potrafi najlepiej generalizować, czyli uogólniać to, czego się nauczyła na podstawie analizy wektorów treningowych, na nowe przypadki. Stopień generalizacji jest sprawdzany na zbiorze testowym, który składa się z wektorów nie występujących w zbiorze treningowym. Generalizacja jest możliwa tylko wtedy, gdy zbiór treningowy jest reprezentatywny dla danego problemu.
W sieci neronowej występują przynajmniej trzy warstwy: wejściowa, ukryta i wyjściowa. Liczba węzłów w warstwie wejściowej jest ustalona na początku procesu uczenia i jest równa wymiarowi wektorów wejściowych. W warstwie wyjściowej występuje tylko jeden węzeł. Liczba węzłów w warstwie ukrytej ulega ciągłemu zwiększeniu. Na początku procesu uczenia istnieją tylko węzły w warstwie ukrytej i wejściowej, następnie w razie potrzeby tzn. gdy nie zostało spełnione kryterium stopu, dostawiane są stopniowo kolejne węzły. Na początku sieć jest konstruowana poprzez dostawianie neuronów, następnie w chwili osiągnięcia pierwszego kryterium stopu następuje uproszczenie sieci, później ponownie występuje douczanie poprzez dostawianie neuronów. Procedura ta jest powtarzana kilkakrotnie, aż do uzyskania wymaganej dokładności działania sieci.
Można oczywiście połączyć systemy logiki rozmytej i sieci neuronowe w jeden system, chociaż niektóre typy sieci neuronowych można i bez tego interepretować jako systemy neurorozmyte.
W rozwinietym przez nas modelu sieci neuronowej FSM (Feature SPace Mapping), możemy każdy z wymiarów (cech) traktować jako niezależny od pozostałych. Funkcje aktywacji neuronów moga być zlokalizowane, tj. osiągające wartość maksymalną w swoim centrum, o wartościach malejących do zera w miarę oddalanie się od tego centrum, np. mogą to być funkcje o kształcie dzwonowym (Gaussa), trapezoidalnym i prostokątnym lub bircentralnym, o kształcie wygładzonych trapezów. Wybór funkcji zależy od celu, jaki sobie stawiamy. Najlepsze rezultaty, zarówno pod względem złożoności sieci jak i jej zdolności do generalizacji, otrzymuje się zwykle dla funkcji gaussa. Funkcje prostokątne używana są do tworzenia klasycznych reguł logicznych. Używając funkcji gaussa, trapezoidalnych lub biradialnych, można za pomocą sieci FSM uzyskać również reguły logiki rozmytej, ale ich interpretacja jest trudniejsza niż reguł klasycznych.
Należy znaleźć prosty opis w postaci reguł logicznych podsumowujący najważniejsze związki pomiedzy wynikami testów i obserwacji a przewidywaniami lub diagnozami. można to zrobić za pomocą systemów uczących się
Przykład: Iris, grzyby
Przykład: wyniki dla baz medycznych.
choroby tarczycy: badania screeningowe.
3772 przypadków zbadano w jednym roku, 3428 z drugiego roku uznano za testowe.
Rozkład klas: niedoczynność 93 przypadki, nadczynność 191 i normalne 3488 (2.47%, 5.06%, 92.47%)
Testowe: niedoczynność 73, nadczynność 177 i normalne 3178 (2.13%, 5.16%, 92.71%)
21 testów (15 tak/nie, 6 ciągłych); 3 klasy
Reguły z systemu C-MLP2LN (wartości ciągłe są pomnożone przez 1000)
Początkowe:
primary hypothyroid: TSH>6.1 & FTI <65
compensated
: TSH > 6 & TT4<149 & On_Tyroxin=FALSE & FTI>64 &
surgery=False
ELSE normal
Reguły po optymalizacji: 4 błędy na zbiorze treningowym (99.89%), 22 na testowym (99.36%)
primary hypothyroid: TSH>30.48 & FTI <64.27
(97.06%)
primary hypothyroid: TSH=[6.02,29.53] & FTI <64.27
& T3< 23.22 (100%)
compensated : TSH > 6.02 & FTI>[64.27,186.71] & TT4=[50, 150.5) &
On_Tyroxin=no & surgery=no (98.96%)
no hypothyroid :
ELSE (100%)
Porównania dokładności przewidywań.
Najbardziej ambitny system ekspercki oparty na regułach zawartych w bazie wiedzy o świecie - realizowany od 1984 roku
Zdrowy rozsądek wymaga milionów reguł! Czy to realne?
Do końca 1990 roku system CYC zawierał około 2 milionów reguł.
Pierwsze milion reguł dotyczy spraw ogólnych, klasyfikacji, ograniczeń, takich pojęć jak czas, przestrzeń, substancja - podstawowa ontologia.
Język reprezentacji wiedzy CycL, oparty na ramach, dla których zdefiniowano rachunek predykatów + zmienne domyślne.
Dziedziczenie przez cały łańcuch relacji.
Dodatkowo: specyfikacja ograniczeń (constraint language).
Reprezentacja obiektów, zdarzeń, nastawień, przekonań.
Wszystko jest rodzajem rzeczy, konkretnej lub abstrakcyjnej.
Rzeczy indywidualne, np. Jan, Polska, nos Jana, mogą mieć części.
Kolekcje = zbiory rzeczy, np. osoba, naród, nos, mogą mieć podzbiory.
Rzeczy nienamacalne nie mają masy, są to zdarzenia, liczby, prawa.
Rzeczy namacalne mają masę, np. ciało człowieka, jabłko czy kurz.
Rzeczy złożone - cechy namacalne i nienamacalne, np. osoba ma ciało i umysł.
Substancja to ObiektIndywidualny, pocięta zachowuje własności.
Specyficzne mechanizmy wnioskowania, ponad 20, zależnie od dziedziny, mikroteorie.
Reguły typu if-needed rule, oraz typu if-added rule, oceniane w nocy.
Spójność wiedzy - truth maintance system.
Poziom epistemologiczny (EL).
Zastosowania:
1995 firma komercyjna
CyCorp
KBNLP czyli Knowledge Based Natural Language Processing system.
The Cycic Friends Network
Przykładowe wyniki dla danych psychometrycznych.
Inne nasze projekty: system HEPAR.
Uczenie maszynowe w zastosowaniu do diagnozy i prognoz raka (Wisconsin)
Grupa LCS Clinical Decision Making z MIT
Wydział Cybernetyki Medycznej (Wiedeń)
Medyczne Systemy Eksperckie (Wiedeń)
Krótki Kurs Informatyki Medycznej (Stanford)
Stanford Medical Informatics
Guardian czyli anioł stróż ze Stanfordu.
Przykłady zastosowań systemów eksperckich w medycynie.
Włodzisław Duch, ostania zmiana 29.05.1999